Question

Problem 7:

A car travels 22 km south, 12 km west, and 14 km north in half an hour.
a) What is the average speed of the car?
b) What is the final displacement of the car?
c) What is the average velocity of the car?​

Answer 1

a) 96 km/h

The average speed can be calculated as the ratio between the total distance covered and the time taken:

`v=(d)/(t)`

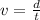
where:

- the total distance is the total length of the path covered, regardless of the direction, so:

d = 22 km + 12 km + 14 km = 48 km

- total time:

t = 0.5 h

So, the average speed is

`v=(48)/(0.5)=96 km/h`

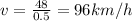
b) 14.4 km, at 33.7 degrees south of west

To find the displacement, we have to compute the net displacements along the two directions (north-south and east-west)

North-south direction (taking north as positive and south as negative):

`d_y = 14 km + (-22 km) = -8 km` (south)

East-west direction (taking east as positive):

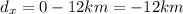`d_x = 0-12 km = -12 km` (west)

So the net displacement is given by Pythagorean's theorem:

`d=√(d_x^2 +d_y^2)=√((-8)^2+(-12)^2)=14.4 km`

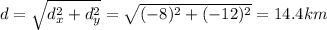
And the direction is given by

`\theta=tan^(-1)((d_y)/(d_x))=tan^(-1)((8)/(12))=33.7^(\circ)`

And the direction is south-west, so this is 33.7 degrees south of west

c) 28.8 km/h at 33.7 degrees south of west

The average velocity is the ratio between the net displacement and the time taken:

`v=(d)/(t)`

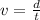
where we have:

displacement: d = 14.4 km

time taken: t = 0.5 h

So, the average velocity is

`v=(14.4)/(0.5)=28.8 km/h`

And the direction is the same as the displacement.