Answer: 6.65 rad/s
Step-by-step explanation:
Firstly, we need to know that according the kinetic theory of gases, the average kinetic energy
 of a molecule with
of a molecule with
 degrees of freedom is:
degrees of freedom is:
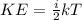 (1)
(1)
Where:
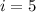 because oxigen is a diatomic molecule and has 5 degrees of freedom
because oxigen is a diatomic molecule and has 5 degrees of freedom
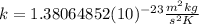 is the Boltzman constant
is the Boltzman constant
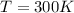 is the temperature
is the temperature
Then:
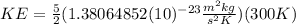 (2)
(2)
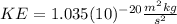 (3) With this value of average kinetic energy we can find the average angular velocity, with the following equation:
(3) With this value of average kinetic energy we can find the average angular velocity, with the following equation:
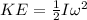 (4)
(4)
Where:
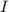 is the moment of inertia
is the moment of inertia
 is the angular velocity
is the angular velocity
Now,
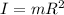 (5)
(5)
Being
 the molar mass of Oxigen molecule and
the molar mass of Oxigen molecule and
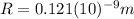 the distance between atoms
the distance between atoms
 (6)
(6)
 (7)
(7)
Substituting (7) and (3) in (4):
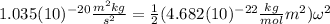 (8)
(8)
Finding
 :
:
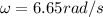 (9) This is the average angular velocity for a molecule of O2
(9) This is the average angular velocity for a molecule of O2