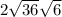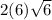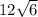Question

The area of a 60-degree sector of a circle is 36π cm^2. What is the diameter of the circle? Explain too, please.

Answer 1

Unsimplified:
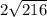`2√(216)` cm

Simplified:
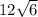`12√(6)` cm

Rounded to nearest tenths: 29.4 cm

Rounded to nearest hundredths: 29.39 cm

Rounded to nearest thousandths: 29.394 cm

Rounded to nearest ten-thousandths: 29.3939 cm

Explanation:

The area of a circle with radius,
`r`, is
`A=\pi r^2`.

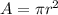Since we have a 60 degree sector with radius
`r` then we have
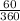`(60)/(360)` of the area of a circle with radius
`r`.

That is we have the following for the area of a 60 degree sector:

`(60)/(360) \cdot \pi r^2`

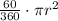
Reduce the fraction:

`(1)/(6) \cdot \pi r^2`

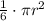
We have that this equals
`36\pi=(1)/(6)\pi r^2`.

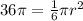This implies
`36=(1)/(6)r^2`.

Multiply both sides by 6:

`216=r^2`

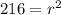
If you take the square root of both sides, you get:

`\pm √(216)=r`

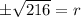
The radius only makes sense to be positive so we can throw the negative out.

`r=√(216)`.

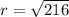So the radius is
`√(216)`.

The diameter is twice the radius. Our diameter is therefore
`2(√(216))=2√(216)`.

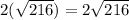We should really go ahead and attach the units.

The answer is
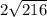`2√(216)` cm.

We can simplify this.

`2√(36)√(6)`

`2(6)√(6)`

`12√(6)`