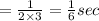Question

An object of mass 100 grams hangs from a long spring. When pulled down 10 cm from its equilibrium position and released from rest, it vibrates with a period of 2 seconds.(a) What is the speed of the object as it passes through the equilibrium position?

b) What is the acceleration of the object when it is 5 cm above the equilibrium position?

c) When it is moving upward, how long does it take for the object to move from a point 5 cm below its equilibrium position to a point 5 cm above its equilibrium position?

Answer 1

(a) 0.314 m/sec (b) 0.492
`m/sec^2` (c)
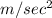`(1)/(6)sec`

Step-by-step explanation:

We have given the mass of object m = 100 gram =0.1 kg

Amplitude A = 10 cm = 0.1 m

Time period T = 2 seconds

We know that
`T=(2\pi )/(\omega )`

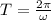
So
`\omega =(2\pi )/(T)=(2\pi )/(2)=\piradian/sec`

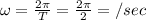
(A) Velocity is given by
`V=A\omega =0.1* 3.14=0.314m/sec`

(b) Acceleration when the object is 5 cm above the equilibrium position
`a=\omega ^2x=3.14^2* 0.05=0.492m/sec^2`

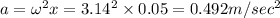
(c) The equation of the motion is given by
`x(t)=Asin(\omega t)`

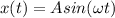
At x =0.05 m

`0.05=0.1sin(3.14t)`

`(1)/(3)sec`

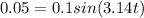
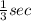
So total time
`= (1)/(2* 3)=(1)/(6)sec`