Answer:
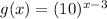
Explanation:
* Lets explain how to solve the problem
- The form of the exponential function is
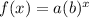 , where
, where
a is the initial amount (x = 0) , b is the growth factor
- If b > 1 , then the function is exponential growth function
- If 0 < b < 1 , then the function is exponential decay function
- If the function translated horizontally by h units to the right , then
the new function is
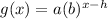
- If the function translated horizontally by h units to the left , then
the new function is
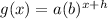
- If the function translated vertically by k units up , then the new
function is
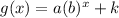
- If the function translated vertically by k units down , then the new
function is
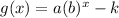
* Lets solve the problem
∵ f(x) is an exponential function
∵ Points (0 , 1) , (1 , 10) , (2 , 100) belong to f(x)
- g(x) is the image of f(x) after translation
∵ Points (3 , 1) , (4 , 10) , (5 , 100) belong to g(x)
∵ point (0 , 1) on f(x) becomes (3 , 1) on g(x)
∵ point (1 , 10) on f(x) becomes (4 , 10) on g(x)
∵ point (2 , 100) on f(x) becomes (5 , 100) in g(x)
∵ All the y-coordinates of the points on the function f(x) are the same
with the y-coordinates of the points on the function g(x)
∴ There is no vertical translation
∵ The x-coordinates of the points on the function f(x) are added by
3 units to give the x-coordinates of the points on the function g(x)
∴ f(x) is translated 3 units to the right
∵
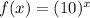
∴
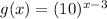
- Look to the attached graph for more understand
# Red graph represents f(x)
# Blue graph represents g(x)