Question

Consider a waveform y(x,t) 15sin(6-7x) which is propagating down a string of unknown material, where y and x are in meters and in seconds. What are (a) the r frequency in Hertz, (b), the radian frequency w, (c) the wavelength, (d) the wavenumber, and (e) the speed of sound for this string's material. (f If we only change the material to a copper string (15.75 m/s), how does the speed of sound change?

Answer 1

Step-by-step explanation:

The wave equation which is propagating down a string of unknown material is given by :

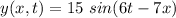`y(x,t)=15\ sin(6t-7x)`................(1)

The general equation of wave is given by :

`y=A\ sin(\omega t-kx)`..............(2)

Comparing equation (1) and (2) we get:

(a)
`\omega=6`

`2\pi f=6`

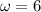
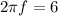
f = 0.954 Hz

(b) Radian frequency,
`\omega=6\ rad/s`

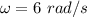
(c) k = 7

`(2\pi)/(\lambda)=7`

`\lambda=0.89\ m`

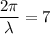
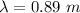
(d) Wave number,
`k=5\ m^(-1)`

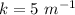
(e) Speed of sound,
`v=f* \lambda`

`v=0.954* 0.89`

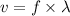
v = 0.849 m/s

Hence, this is the required solution.