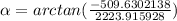Question

A series AC circuit contains a resistor, an inductor of 220 mH, a capacitor of 5.50 μF, and a generator with ΔVmax = 240 V operating at 50.0 Hz. The maximum current in the circuit is 140 mA. a. Calculate the inductive reactance.Ω

b.Calculate the capacitive reactance.Ω
c. Calculate the impedance.kΩ
d.Calculate the resistance in the circuit.kΩ
e. Calculate the phase angle between the current and the generator voltage.

Answer 1

`Xl=wL=69.11503383 ohm`

`Xc=(-1)/(wC)= -578.7452476 ohm`

`Z=(240)/(140*10^-3)=1.714285714 kilo-ohm`

`R=2.223915928 kilo-ohm`

`\alpha = -12.90698798 centigrades`

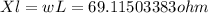
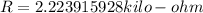
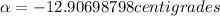
Step-by-step explanation:

`L=220*10^-3`

`C=5.50*10^-6`

`Vmax=240V`

`Imax=140*10^-3`

`w=2\pi f=2\pi *50=314.1592654`

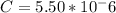
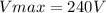
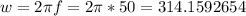
The capacitive reactance is given by:

`Xc=(-1)/(wC)=-578.7452476 ohm`

Now, The inductive reactance is given by:

`Xl=wL=69.11503383 ohm`

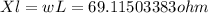
By the ohm´s law, the electrical impedance is:

`V=IZ`

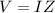
So

`Z=(V)/(I)`

`Z=(240)/(140*10^-3)=1.714285714 kilo-ohm`

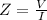
The total impedance is:

`Z=R+jX\\\\` (*)

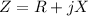Where X is the total reactance given by:

`X=Xl+Xc=69.11503383-578.7452476=-509.6302138`

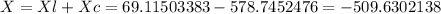
Let´s calculate the real part of Z using (*):

`R=1714.285714+509.6302138`

`R=2.223915928 kilo-ohm`

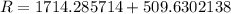
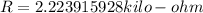
Finally the angle between the current and the voltage is equal to the impedance angle:

`\alpha=arctan((-509.6302138)/(2223.915928))`

`\alpha =-12.90698798 centigrades`