Question

A blue supergiant star has surface temperature 27 kK and has total power output 100000 times that of the Sun.

a. Where is the Wien peak of this star's blackbody curve?​ λmax =

b. Given the Sun's 6.96×108m radius, what's the radius of the supergiant? r =

Answer 1

Wien peak ( λmax ) is 107.40 nm

radius of super giant is 1.086 ×
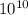`10^(10)` m

Step-by-step explanation:

given data

temperature 27 kK

power = 100000 times of Sun

Sun radius = 6.96 × 10^8 m

to find out

Wien peak ( λmax ) and radius of supergiant (r)

solution

we will apply here first wien law to find Wien peak that is

λmax = b / t

λmax = 2.9 ×
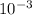`10^(-3)` / 27000 = 1.0740 ×
`10^(-7)`

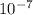
so Wien peak ( λmax ) is 107.40 nm

and

now we apply steafay law that is

P = σ × A ×
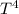`T^(4)` .........................1

and we know total power output 100000 time of Sun

so we say

4πr²s
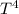`T^(4)` = 100000 × 4πR²s
`Ts^(4)`

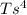
r² = 100000 × R²
`Ts^(4)` /
`T^(4)`

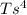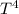
put here value

r² = 100000 × (6.96×
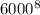`6000^(8)` )² ×
`6000^(4)` /
`27000^(4)`

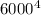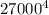
r² = 1.18132 ×
`10^(20)`

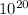
r = 1.086 ×
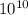`10^(10)` m

so radius of super giant is 1.086 ×
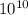`10^(10)` m