Answer and Explanation:
We have given the expression
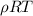
Dimension of
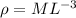
Dimension of R which is gas constant
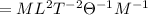
Dimension of temperature T
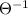
And dimension of pressure
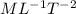
Now combine dimension of
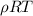
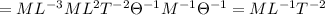
So the dimension of
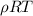 and dimension P is same so there unit will also be same
and dimension P is same so there unit will also be same
From ideal gas equation we know that
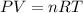
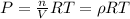
As the both P and
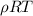 has same dimension so they are dimensionally constant
has same dimension so they are dimensionally constant