Question

Calculate the radius of the orbit of a proton moving at 2.2x10^6 m/s in a magnetic field 0.7 T where v and B are perpendicular. Give your answer in centimetres.

Answer 1

3.28 cm

Step-by-step explanation:

To solve this problem, you need to know that a magnetic field B perpendicular to the movement of a proton that moves at a velocity v will cause a Force F experimented by the particle that is orthogonal to both the velocity and the magnetic Field. When a particle experiments a Force orthogonal to its velocity, the path it will follow will be circular. The radius of said circle can be calculated using the expression:

r =
`(mv)/(qB)`

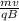
Where m is the mass of the particle, v is its velocity, q is its charge and B is the magnitude of the magnetic field.

The mass and charge of a proton are:

m = 1.67 * 10^-27 kg

q = 1.6 * 10^-19 C

So, we get that the radius r will be:

r =
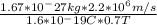`(1.67 * 10^-27 kg * 2.2*10^6 m/s)/(1.6 * 10^-19 C* 0.7 T)` = 0.0328 m, or 3.28 cm.