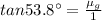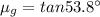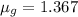Question

Determine the index of refraction of glass that is struck by unpolarized light at 53.8 degrees and resulting in a fully polarized reflected beam. (Brewster angle).

Answer 1

The refractive index of glass,
`\mu_(g) = 1.367`

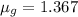
Solution:

Brewster angle is the special case of incident angle that causes the reflected and refracted rays to be perpendicular to each other or that angle of incident which causes the complete polarization of the reflected ray.

To determine the refractive index of glass:

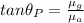`tan\theta_(P) = (\mu_(g))/(\mu_(a))` (1)

where

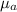`\mu_(a)` = refractive index of glass

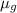`\mu_(g)` = refractive index of glass

Now, using eqn (1)

`tan{53.8^(\circ)} = (\mu_(g))/(1)`

`\mu_(g) = tan53.8^(\circ)`

`\mu_(g) = 1.367`