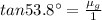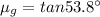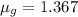Answer:
The refractive index of glass,
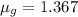
Solution:
Brewster angle is the special case of incident angle that causes the reflected and refracted rays to be perpendicular to each other or that angle of incident which causes the complete polarization of the reflected ray.
To determine the refractive index of glass:
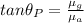 (1)
(1)
where
 = refractive index of glass
= refractive index of glass
 = refractive index of glass
= refractive index of glass
Now, using eqn (1)