Answer:
True options:
1. The vertex of the function is at (1,–25).
5. The graph is negative on the entire interval –4 < x < 6.
Explanation:
Part of the graph of the function f(x) = (x + 4)(x – 6) is shown in attached diagram.
This graph intesects the x-axis at points (-4,0) and (6,0). So, the x-coordinate of the vertex is

The y-coordinate of the vertex is

Hence, the vertex is ar the point (1,-25) - frist option is true, second option is false.
For all
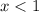 the graph is decreasing, for all
the graph is decreasing, for all
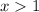 the graph is increasing. So, third option is false.
the graph is increasing. So, third option is false.
The graph is positive (placed above the x-axis) for all
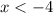 or
or
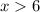 . This means fourth option is false.
. This means fourth option is false.
The graph is negative (placed below the x-axis) for all
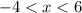 . This means fifth option is true.
. This means fifth option is true.