Question

A particle of unknown mass is in a 1-dimensional box of width L = 3.0 x 10-10 m with infinitely high potential walls at x = 0 and at x = L, and zero potential for 0 < x < L. The particle is in the second excited state of the box. What is the de Broglie wavelength, ?, of the particle?

Answer 1

0.2 nm

Step-by-step explanation:

As we know that the energy of the nth level of one dimensional potential box is,

`E_(n)=(h^(2)n^(2))/(8mL^(2) )`

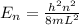
And also it is known that,

`E=(p^(2) )/(2m)`

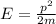
Put this in the above equation.

`(p^(2) )/(2m)=(h^(2)n^(2))/(8mL^(2) )\\p=(hn )/(2L)`

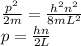
Now, de Broglie wavelength is,

`\lambda=(h)/(p)`

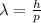
Therefore,

`\lambda=(h2L)/(n h ) \\\lambda=(2L)/(n )`

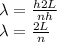
Given that, the width of 1 dimension box is,

`L=3* 10^(-10)m`

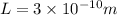
For the second excited state n=3,

`\lambda=(2* 3* 10^(-10)m)/(3)\\\lambda=2* 10^(-10)m\\\lambda=0.2nm`

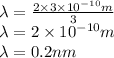
De Broglie wavelength of the particle is 0.2 nm.