Question

The functions f(x) = -(x-1)^2 + 5 and g(x) = (x+2)^2 - 3 have been rewritten using the completing-the-square method. Is the vertex for each function a minimum or a maximum? Explain your reasoning for each function.

Answer 1

a) f(x) has a maximum vertex

b) g(x) has a minimum vertex

Explanation:

The function

`p(x) = a(x - h)^(2) + k`

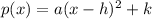
has its vertex at (h,k).

If a>0, then (h,k) is a minimum vertex.

If a<0, then (h,k) is a maximum vertex.

The first function is

`f(x) = - (x - 1)^(2) + 5`

a=-1<0, therefore the vertex (1,5) is the maximum point.

The second function is

`g(x) = {(x + 2)}^(2) - 3`

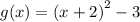
a=1>0, therefore the vertex (-2,-3) is a minimum point.