Question

State whether the following coordinates on a Cartesian plane form an acute, obtuse or right triangle: a) (-1, 1), (7,-2) and (1,-5) --_______ b) (0,6), (1, 2) and (5,3) ___

Answer 1

a) Acute triangle

b) Right triangle

Explanation:

∵ A triangle having sides a, b and c is called,

Acute : If a² + b² > c² or a² + c² > b² or b² + c² > a²,

Obtuse : if a² + b² < c² or a² + c² < b² or b² + c² < a²

Right : a² + b² = c² or a² + c² = b² or b² + c² = a²,

a) Let A≡(-1, 1), B≡(7,-2) and C≡(1,-5),

By the distance formula,

`AB=√((7-(-1))^2+(-2-1)^2)=√((7+1)^2+(-3)^2)=√(8^2+3^2)=√(64+9)=√(73)\text{ unit}`

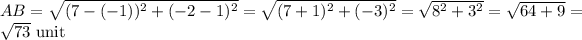
Similarly,

`BC=√(45)\text{ unit}`

`CA=√(40)\text{ unit}`

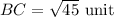
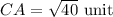
∵ The sum of any two sides is greater than third side,

So, ABC is a triangle,

Now,

`AB^2 + BC^2 > CA^2`

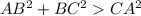
⇒ ABC is an acute triangle.

b) Let P≡(0,6), Q≡(1,2) and R≡(5,3),

By the distance formula,

PQ = √17 unit,

QR = √17 unit,

RP = √34 unit,

∵ The sum of any two sides of PQR is greater than third side,

⇒ PQR is a triangle ,

Also,

`RP^2=PQ^2+QR^2`

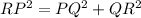
Hence, PQR is a right triangle.