Question

An unknown gas occupies a volume of 4.75 L at 1227 "Cand 5.00 atm. If the mass is 5.45 g what is the molar mass of the gas? (R=0.0821 atmL/molK) A) 23.8 g/mol B) 344 g/mol C) 215 g/mol D) 28.3 g/mol E) 141 g/mol

Answer 1

Answer : The correct option is, (D) 28.3 g/mole

Explanation :

Using ideal gas equation :

`PV=nRT\\\\PV=(w)/(M)RT`

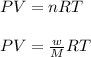
where,

P = pressure of gas = 5.00 atm

V = volume of gas = 4.75 L

T = temperature of gas =
`1227^oC=273+1227=1500K`

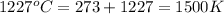
n = number of moles of gas

w = mass of gas = 5.45 g

M = molar mass of gas = ?

R = gas constant = 0.0821 L.atm/mol.K

Now put all the given values in the ideal gas equation, we get:

`(5.00atm)* (4.75L)=(5.45g)/(M)* (0.0821L.atm/mol.K)* (1500K)`

`M=28.3g/mole`

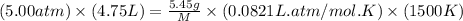
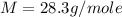
Therefore, the molar mass of the gas is 28.3 g/mole

Answer 2

(d) 28.3 g/mol

Step-by-step explanation:

We have given the volume V = 4.75 L

Pressure = 5 atm

Mass in gram = 5.45 gram

R = 0.02821 atmL/molK

Temperature T =1227°C=1227+273=1500 K

From ideal gas equation PV=nRT

`5* 4.75=n* 0.0821* 1500`

`n=0.1928`

We know that
`n=(mass\ in\ gram)/(molar\ mass)`

So molar mass
`=(mass\ in\ gram)/(n)=(5.45)/(0.1928)=28.25g/mol`