Question

A ball of mass 2 kg moving at 6 m/s collides directly with another ball of mass 3 kg travelling in the same direction at 4 m/s. Find the speed of each ball after impact and the loss in kinetic energy if the coefficient of restitution is equal to 3/4.

Answer 1

v₁ = 3.9 m/s

v₂ = 5.4 m/s

The loss in the kinetic energy = 1.05 J

Step-by-step explanation:

Given:

mass, m₁ = 2 kg

m₂ = 3 kg

initial speed of mass m₁, u₁ = 6 m/s

Initial speed of the mass m₂, u₂ = 4 m/s

coefficient of restitution, e = (3/4)

let, the final speed of mass m₁ and m₂ be v₁ and v₂ respectively

Now,

`e=(v_2-v_1)/(u_1-u_2)\\`

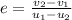
on substituting the values, we get

`(3)/(4)=(v_2-v_1)/(6-4)\\`

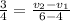
or

1.5 = v₂ - v₁

or

v₂ = 1.5 + v₁

also,

from the conservation of momentum, we have

( 2 × 6 ) + ( 3 × 4 ) = ( 2 × v₁ ) + ( 3 × v₂ )

or

24 = 2 × v₁ + ( 3 × ( 1.5 + v₁ ) )

or

24 = 2 × v₁ + 4.5 + 3 × v₁

19.5 = 5 × v₁

or

v₁ = 3.9 m/s

and

v₂ = 1.5 + v₁

or

v₂ = 1.5 + 3.9

or

v₂ = 5.4 m/s

now,

the loss in the kinetic energy = initial kinetic energy - Final kinetic energy

or

=
`((1)/(2)m_1u_1^2+(1)/(2)m_2u_2^2)-((1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2)`

or

=
`((1)/(2)*2*6^2+(1)/(2)*3*4^2)-((1)/(2)*2*3.9^2+(1)/(2)*3*5.4^2)`

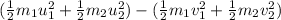
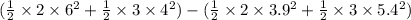
or

the loss in the kinetic energy = 1.05 J