Answer:
The optimum order size is 2,070 units.
Step-by-step explanation:
For computing the optimum order size, we have to compute the economic order quantity which is shown below:
=

where,
annual demand is 60,000
Ordering cost is 25 per order
and carrying cost is 0.70 per unit
Now put the values to the above formula
So, the answer would be
=
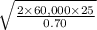
= 2,070 units
Hence, the optimum order size is 2,070 units.