Question

find the pressure gradient of a capillary tube with radius 0.514*10^-3 m when volume of water flowing through it is 7.06 cm^3 per min. coeff of viscosity=0.00138 Pa *s

Answer 1

5923.7 Pa/m

Step-by-step explanation:

radius of capillary tube, r = 0.514 x 10^-3 m

Volume of flow, V = 7.06 cm^3/min = 1.176 x 10^-7 m^3/s

viscosity, η = 0.00138 Pa s

By use of Poiseuillie's law

`V = (\pi P*r^(4))/(8\eta* l)`

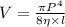
Where, V be the volume flow per second and l be the length of the tube

So, pressure gradient

`(P)/(l) = \frac{8\eta V}}{\pi r^(4)}`

`(P)/(l) = \frac{8 * 0.00138 * 1.176 * 10^-7}}{3.14 * 0.514^(4) * 10^(-12)}`

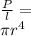
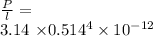
P/l = 5923.7 Pa/m