Question

A pair of thin spherical shells with radius r and R, r < R are arranged to share a center. What is the capacitance of the system. If a potential difference V is created between the shells, how much energy is stored between them?

Answer 1

Capacitance = ( 4π×∈×r×R ) / (R-r)

energy store = ( 4π×∈×r×R )×V² / (R-r)

Step-by-step explanation:

given data

radius = r

radius = R

r < R

to find out

capacitance and how much energy store

solution

we consider here r is inner radius and R is outer radius

so now apply capacitance C formula that is

C = Q/V .................1

here Q is charge and V is voltage

we know capacitance have equal and opposite charge so

V =
`\int\limits^R_r {E} \, dx`

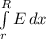
here E = Q / 4π∈k²

so

V = Q / 4π∈
`\int\limits^R_r {1/k^2} \, dx`

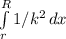
V = Q / 4π∈ × ( 1/r - 1/R )

V = Q(R-r) / ( 4π×∈×r×R )

so from equation 1

C = Q/V

Capacitance = ( 4π×∈×r×R ) / (R-r)

and

energy store is 1/2×C×V²

energy store = ( 4π×∈×r×R )×V² / (R-r)