Question

A random sample of house sizes in major city has a sample mean of x¯=1204.9 sq ft and sample standard deviation of s=124.6 sq ft. Use the Empirical Rule to determine the approximate percentage of house sizes that lie between 955.7 and 1454.1 sq ft

Answer 1

Answer: 95%

Explanation:

The Empirical rule says that about 68% of the data is within one standard deviation of the mean; about 95% of the data is within two standard deviations of the mean ; about 99.7% of the data is within three standard deviations of the mean.

Given : Sample mean :
`\overline{x}=1204.9\text{ sq.ft.}`

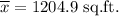
Standard deviation:
`s=124.6\text{ sq. ft.}`

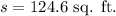
To find the percentage of house sizes that lie between 955.7 and 1454.1 sq ft.

We can write it as
`955.7=1204.9-249.2=1204.9-2(124.6)`

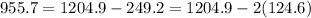
and
`1454.1=1204.9+249.2=1204.9+2(124.6)`

Thus, 955.7 is 2 standard deviations left from the means and 1454.1 is 2 deviations right from the mean.

Then by empirical rule , about 95% of house sizes that lie between 955.7 and 1454.1 sq ft .