Question

A teacher pulls a box of books on a horizontal floor with a force of 207 N directed 46.7° above the horizontal. The coefficient of kinetic friction between the box and the floor is μk = 0.222. The mass of the box and books is 43.7 kg. a. Draw a free-body diagram for the box. b. What is the normal force that the floor exerts on the box? c. Calculate the acceleration of the box.

Answer 1

Step-by-step explanation:

Given that,

Mass of the box an books = 43.7 kg

Coefficient of kinetic friction = 0.222

Force = 207 N

Angle = 46.7°

(A). we draw the free body diagram

(B). We need to calculate the normal force

Using formula of normal force

∑y=0

`N+f\sin\theta=mg`

`N=mg-f\sin\theta`

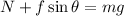
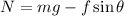
Put the value into the formula

`N=43.7*9.8-207\sin46.7`

`N=277.61\ N`

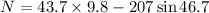
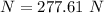
The normal force that the floor exerts on the box is 277.61 N.

(c). We need to calculate the acceleration of the box

Using formula of acceleration

`\Sigma F_(x)=ma`

`F\cos\theta-f_(k)=ma`

`a=(F\cos\theta-\mu_(k)N)/(m)`

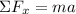
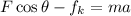
Put the value into the formula

`a=(207\cos46.7-0.222*277.61)/(43.7)`

`a=1.84\ m/s^2`

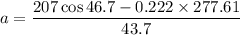
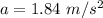
The acceleration of the box is 1.84 m/s².

Hence, This is the required solution.