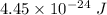Answer :
The energy difference between parallel and anti parallel alignment of the z component of an electron's spin is
Explanation :
Given that,
Magnetic field = 0.24 T
We need to calculate the energy difference between parallel and anti parallel alignment of the z component of an electron's spin
Using formula of energy difference between parallel and anti parallel alignment
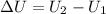
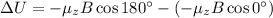
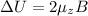
We know that,
The value of Bohr magneton is given by

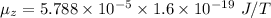
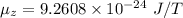
Put the value into the formula
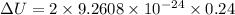
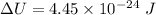
Hence, The energy difference between parallel and anti parallel alignment of the z component of an electron's spin is