Answer:
2401
Step-by-step explanation:
The amount of power radiated by an object can be calculated with the Stefan-Boltzmann law, this law is expressed as:

- P = total power radiated.
- A = surface area.
 = emissivity.
= emissivity.
 = Stefan-Boltzmann constant.
= Stefan-Boltzmann constant.- T = temperature of the object (in degrees Kelvin).
In this problem, it's supposed that we move from state 1
(
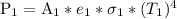 )
)
where all the variables are known, to state 2, where
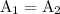 ,
,
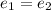 ,
,
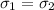 , and T is 7 times bigger than before, so to find
, and T is 7 times bigger than before, so to find
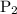 we have the replace
we have the replace
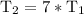 .
.
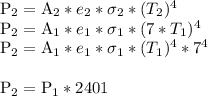
This means that the amount of power radiated is multiplied by 2401.