Answer:
E(0.1m)=-16.53.10^6 V.m
E(0.465m)=-3.55.10^6 V.m
E(1.3m)=-1.27^6 V.m
Step-by-step explanation:
You can find the field using Gauss's Law:
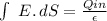
the surface S is an "infinite long" cylinderr of radio r.
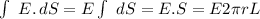
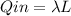
E(r)=
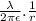
λ=-92.0 μC/m, ε=8.85.10^-12
E(0.1m)=-16.53.10^6 V.m
E(0.465m)=-3.55.10^6 V.m
E(1.3m)=-1.27^6 V.m