Answer:
J'(2,-3), K'(4, -3) and L'(5,-2)
Explanation:
The given triangle has vertices at J(2,3), K(4, 3) and L(5,2).
The transformation rule for a reflection in the x-axis is:
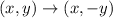
We substitute the points to obtain the coordinates of the image triangle J'K'L'
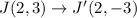
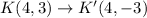
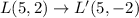
In other words, we negate the y-coordinates of triangle JKL to obtain the coordinates of J'K'L'
See attachment for graph.