Answer:

Step-by-step explanation:
We want to know the value of
 when
when

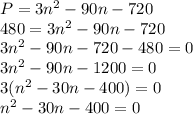
From here, we can find the factors of the quadratic equation, we need two numbers that multiplied give -400 and added -30. Since they are factors of 400, we can choose -20x20 or -40x10. When adding -20 and 20 the result is zero, but the sum of -40 and 10 is -30. Then:
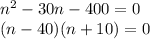
The solutions of the quadratic equation are
 and
and
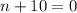 :
:
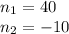
Since
 is a positive integer:
is a positive integer:
