Answer:
28,8 m/s
Step-by-step explanation:
In a steady flow system we can say that m1=m2 which means that the mass flow in the entrance in the same in the outlet. m is flow (kg/s)
we know that
 where V (m/s) is velocity, A (m^2) ia area and v is specific volume (m^3/kg)
where V (m/s) is velocity, A (m^2) ia area and v is specific volume (m^3/kg)
Since m1=m2 we can say
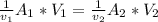
clearing the equation

we can specific volume (m^3/kg) from thermodynamic tables
for the entrance is 400°C and 4 MPa is superheated steam and v is : 0,7343 m^3/kg
In the outlet we have saturated vapor with quality (x) of 80%. In this case we get the specific saturated volume for the liquid (vf) and the specific volume for the saturated (vg) gas from the thermodynamic tables. we use the next equation to get (v) for the condition of interest, in this case 80% quality.
v= vf +x*(vg - vf)
where:
x: quality
vf = liquid-saturated-specific-volume
vg =steam-saturated-specific-volume.
for this problem
x = 0,8
vf = 0,00102991
vg = 3,24015
so
we get = 2,593 m^3/kg
The area is the one for a circle
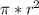
r1 = 0,1 m^2 for area 1
r2=0,5 m^2 for area 2
A1 = 0,0314 m^2
A2 = 0,7853 m^2
we know that V1 is 20 m/s
replacing these values in the equation

we get V2 = 28,2 m/s.