Question

You're in a car that gets 37 miles per gallon of gas, driving it at a constant speed. If you took the gas from the car tank, and instead filled a long cylinder or hose alongside the car's path, what would the diameter of the hose need to be?

Answer 1

Required diameter of hose pipe = 0.2864 mm

Solution:

From the continuity eqn, the fluid flow rate is given by:

Av =
`(V)/(t)`

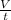
where

A = cross-sectional area =
`\pi r^(2)`

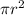
r = hose pipe radius

v = velocity of gas

Also,
`v = (displacement, d)/(time, t)`

Using:

1 gallon = 3.854 l

1 mile = 1609.34 m

`1 m^(3) = 1000 l`

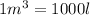
Therefore,

`A(d)/(t) = (V)/(t)`

`\pi r^(2) = (V)/(d)`

`\pi r^(2) = ((1 gal).((3.7854 l)/(gal)).((10^(- 3) m^(3))/(l)))/(37 miles((1609.34 m)/(miles)))`

`6.357* 10^(- 8) = \pi r^(2)`

`r^(2) = 2.024* 10^(- 8)`

`r = 1.423* 10^(- 4) m = 0.1423 mm`

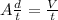
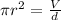
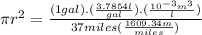
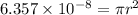
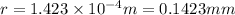
The diameter of the hose pipe = 2r =
`2* 1.423* 10^(- 4)`

The diameter of the hose pipe =
`2.846* 10^(- 4) m = 0.2846 mm`