Answer:
6.21 seconds
Explanation:
The position function of a free-falling object is,
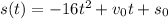
Where,
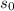 = initial height of the object,
= initial height of the object,
 = initial velocity of the object,
= initial velocity of the object,
Here,
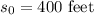
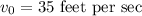
Hence, the height of the ball after t seconds,
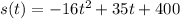
When s(t) = 0,
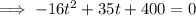
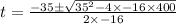

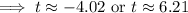
∵ Time cannot be negative,
Hence, after 6.21 seconds the ball will reach the ground.