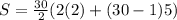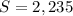Question

Given the sequence 2,7,12,..., write an explicit

formula for the nth term, assuming a1=2.
2 Given the sequence 2,7,12,..., find the sum of
the first 30 terms
​

Answer 1

Part 1)
`a_n=2+5(n-1)`

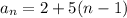
Part 2) The sum of the first 30 terms is 2,235

Explanation:

Part 1) write an explicit formula for the nth term

we know that

In an Arithmetic Sequence the difference between one term and the next is a constant, and this constant is called the common difference

We can write an Arithmetic Sequence as a rule:

`a_n=a_1+d(n-1)`

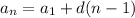
where

`a_n` is the nth term

`a_1` is the first term

n is the number of terms

d is the common difference

we have the sequence

`2,7,12,...`

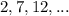
we have

`a_1=2`,
`a_2=7`,
`a_3=12`

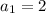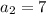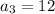
Find the common difference d

`a_2-a_1=7-2=5`

`a_3-a_2=12-7=5`

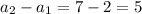
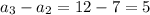
The common difference is d=5

substitute in the formula

`a_n=2+5(n-1)`

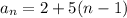
Part 2) Find the sum of the first 30 terms

we know that

The formula to calculate the sum of an arithmetic sequence is

`S=(n)/(2)(2a_1+(n-1)d)`

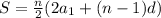
where

`a_1` is the first term

n is the number of terms

d is the common difference

we have

`a_1=2`

`d=5`

`n=30`

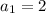
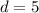
substitute

`S=(30)/(2)(2(2)+(30-1)5)`

`S=2,235`