Question

A block of mass m moving with a velocity v collides with a mass 2m at rest. Consider the collision is elastic, we have to find the final velocities of both masses.

Answer 1

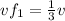`vf_(1) =(1)/(3) v`:Final block velocity (toward the left)

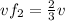`vf_(2) =(2)/(3) v` :Final mass velocity (to the right)

Step-by-step explanation:

To solve this problem we apply the theory of shocks:

In an elastic shock the kinetic energy and the amount of linear movement or momentum are conserved.

Because the shock is elastic, the coefficient of elastic restitution (e) is equal to 1.

Principle of conservation of the momentum:

m1vi1+m2vi2=m1vf1+m2vf2 Equation 1

Formula to calculate the coefficient of elastic restitution (e):

`e=(vf_(2)-vf_(1)  )/(vi_(1)-vi_(2)  )` Equation 2

m1: Block mass

m2: mass of the body that collides with the block

Vi1,vf1: initial, final velocity of the block

Vi2,vf2: initial, final velocity of the body that collides with the block

Of the problem data we know that:

m1=m , m2 = 2m, vi1=v and vi2=0, then, we replace this information in equation (1) :

mv+0=mvf1+2mvf2 we divide by m:

v=vf1+2vf2 Equation (3)

Because the shock is elastic, the coefficient of elastic restitution (e) is equal to 1,then , we we replace this information in equation (2)

`1=(vf_(2)-vf_(1)  )/(v-0)`

v=vf2-vf1 Equation (4)

vf2=v+vf1 Equation (5)

We replace the equation 5 in the equation (3)

v=vf1+2(v+vf1)

v=vf1+2v+2vf1

-3vf1=v

`vf_(1) = -(1)/(3) v`

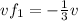
We replace Vf1=(-1/3)v in the equation (5):

`vf_(2) =v-(1)/(3) v`

`vf_(2) =(2)/(3) v`

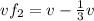
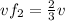
Answer;

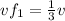`vf_(1) =(1)/(3) v`:Final block velocity (toward the left)

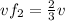`vf_(2) =(2)/(3) v` :Final mass velocity (to the right)