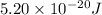Answer : The correct answer is
Explanation :
For green light :
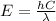
where,
E = energy of green light = ?
h = Planck's constant =
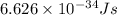
C = speed of light =
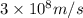
 = wavelength of light = 536 nm =
= wavelength of light = 536 nm =
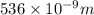
Now put all the given values in the above formula, we get:
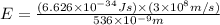
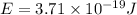
For red light :
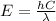
where,
E = energy of red light = ?
h = Planck's constant =
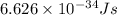
C = speed of light =
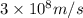
 = wavelength of light = 622 nm =
= wavelength of light = 622 nm =
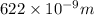
Now put all the given values in the above formula, we get:


Now we have to calculate the energy difference.
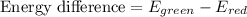
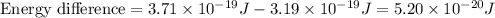
Therefore, the correct answer is