Question

A multiple choice test consists of four questions, each of which has three choices. Each question has exactly one correct answer. How many ways are there to fill out the answer sheet so that three answers are correct and one is incorrect? (Assume that a choice is made for each question.)

Answer 1

12 ways

Step-by-step explanation

First, we will count the number of ways to get three correct answers:

Notice there is a set of 4 correct answers (one per each one of the four questions in the test). We need to pick three of them. The order does not matter (for example: it is the same to have the arrangement of correct answers: Question 1 , Question 2 and Question 3, than having the arrangement: Question 2, Question 1 and Question 3). Therefore, we are dealing with combinations from a set of 4 elements forming groups of 3 elements:

`\displaystyle C^4_3=(4!)/((4-3)!3!)=(4\cdot3!)/(1!3!)=(4)/(1!)=4`

Now we need to count the number of ways we can answer incorrectly the remaining fourth question:

We have a total set of 3*4 = 12 incorrect answers (three per each one of the four questions in the test). But notice that once we have picked three correct answers, then we should exclude from the set of incorrect answers we can pick, those of the three questions already answered. So, we are left with just the set of incorrect answers of the remaining question that has not been responded yet. Thus, we just have 3 incorrect answer to pick for the remaining question.

Then using the fundamental counting principle, we multiply the previous results:

Ways to answer correctly three questions * Ways to answer incorrectly the remaining question

`4\cdot3=12`

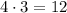
Therefore, there are 12 ways to fill out the answer sheet so that three answers are correct and one is incorrect.