Answer with Step-by-step explanation:
We are given that a function
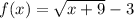
Domain of f(x)=[-9,
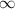 )
)
The inverse of given function
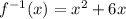
a.We have to find the domain of

We know that domain of f(x) is convert into range of
 and range of f(x) is convert into domain of
and range of f(x) is convert into domain of

If we substitute x=-9 in the given function then we get
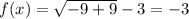
Therefore, range of f(x) =[-3,
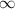 )
)
Domain of
![f^(-1)(x)=[-3,[tex]\infty)](https://img.qammunity.org/2020/formulas/mathematics/high-school/36q9qua834h4pv9srmj8ihzp7o9kvvn7cp.png)
b.Range of f(x) is restricted .Therefore, domain of
 must be restricted because range of f(x) is converted into domain of
must be restricted because range of f(x) is converted into domain of
 and range of f(x) is restricted.
and range of f(x) is restricted.