Question

Suppose matrix product AB is defined. (a) If A is 4 x 7 and B is a column matrix, give the dimensions of B and AB. [4 marks] (b) If A is the identity matrix and B is 5 x 5, what size is A? [4 marks] (c) If A is 4 x 5 and AB is 4 x 7, what size is B?

Answer 1

(a) Order of matrix B is 7 × 1 and order of matrix AB is 4 × 1.

(b) Order of matrix A is 5 × 5.

(c) The order of matrix B is 5 × 7.

Explanation:

The product of two matrices is possible if and only if column of first matrix is equal to row of second matrix.

If A is an n × m matrix and B is an m × o matrix, their matrix product AB is an n × p matrix,

(a)

It is given that order of matrix A is 4 x 7.

B is a column matrix. It means the number of column in matrix B is 1.

Let the order of matrix B = n × 1

Product of matrices A and B is possible if and only if column of matrix A is equal to row of matrix B.

`n=7`

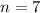
Order of matrix B is 7 × 1

`A_(4* 7)B_(7* 1)=AB_(4* 1)`

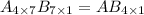
Order of matrix AB is 4 × 1.

(b)

Order of matrix B = 5 × 5

It is given that A is the identity matrix.

Identity matrix is a square matrix having 1s on the main diagonal, and 0s everywhere else.

So, order of matrix A is equal to order of matrix B.

Order of matrix A = 5 × 5

Therefore order of matrix A is 5 × 5.

(c)

Order of matrix A = 4 × 5

Order of matrix AB = 4 × 7

Let Order of matrix B = n × m

`A_(4* 5)B_(n* m)=AB_(4* 7)`

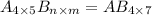
Product of A and B are possible if and only if n=5.

`A_(4* 5)B_(5* m)=AB_(4* 7)`

`AB_(4* m)=AB_(4* 7)`

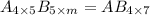
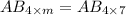
On comparing both sides, we get

`m=7`

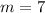
Therefore the order of matrix B is 5 × 7.