Answer:
v = at + u
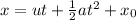
Step-by-step explanation:
acceleration, a = constant
As we know that acceleration is the rate of change of velocity
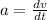
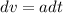
integrate on both sides
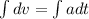
v = at + u
Where, u is the integrating constant and here it is equal to the initial velocity
Now we know that the rate of change of displacement is called velocity
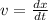
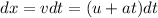
Integrate on both sides
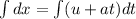
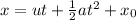
where, xo is the integrating constant which is initial position of the particle.