Question

Given a constant acceleration and assuming linear motion, derive equations for velocity and position of a body with respect to time. Explain what the integration constant represents.

Answer 1

v = at + u

`x = ut+(1)/(2)at^(2)+x_(0)`

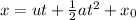
Step-by-step explanation:

acceleration, a = constant

As we know that acceleration is the rate of change of velocity

`a=(dv)/(dt)`

`dv=adt`

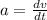
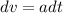
integrate on both sides

`\int dv=\int adt`

v = at + u

Where, u is the integrating constant and here it is equal to the initial velocity

Now we know that the rate of change of displacement is called velocity

`v = (dx)/(dt)`

`dx=vdt=(u+at) dt`

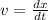
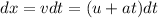
Integrate on both sides

`\int dx=\int (u+at) dt`

`x = ut+(1)/(2)at^(2)+x_(0)`

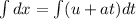
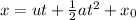
where, xo is the integrating constant which is initial position of the particle.