Question

A firm has the following cost and marginal cost​ functions: Upper C left parenthesis q right parenthesis equals 64 plus q squared and MC equals 2 q. What is the minimum efficient​ scale? The minimum efficient scale LOADING... occurs at nothing units of output ​(enter your response as a whole number​).

Answer 1

Answer: Minimum efficient​ scale is 8 units.

Step-by-step explanation:

Given that,

Cost function: C(q) = 64 +
`q^(2)`

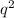
Marginal cost function: MC = 2q

Average cost: AC =
`(C(q))/(q)`

=
`(64 + q^(2))/(q)`

=
`(64)/(q) + q`

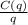
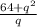
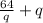
The minimum efficient scale is at a point where MC = AC

2q =
`(64)/(q) + q`

`q^(2) = 64\\q = √(64) \\q = 8`

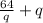
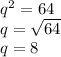
Therefore, minimum efficient​ scale is 8 units.