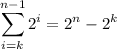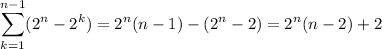Question

Solve the recursion relation an = 2an-1 +n, with a_o = 1.

Answer 1

`\begin{cases}a_0=1\\a_n=2a_(n-1)+n&\text{for }n>0\end{cases}`

By the definition above,

`a_(n-1)=2a_(n-2)+(n-1)`

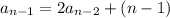
and by substitution we get

`a_n=2(2a_(n-2)+(n-1))+n=2^2a_(n-2)+2(n-1)+n`

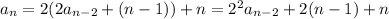
If we keep following this procedure, we'll start to see a pattern:

`a_(n-2)=2a_(n-3)+(n-2)`

`\implies a_n=2^2(2a_(n-3)+(n-2))+2(n-1)+n`

`\implies a_n=2^3a_(n-3)+2^2(n-2)+2(n-1)+n`

`a_(n-3)=2a_(n-4)+(n-3)`

`\implies a_n=2^3(2a_(n-4)+(n-3))+2^2(n-2)+2(n-1)+n`

`\implies a_n=2^4a_(n-4)+2^3(n-3)+2^2(n-2)+2(n-1)+n`

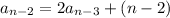
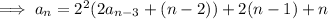
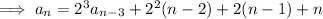
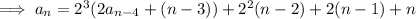
and so on, down to

`a_n=2^na_0+\displaystyle\sum_(i=0)^(n-1)2^i(n-i)`

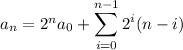
Now,

`\displaystyle\sum_(i=0)^(n-1)2^i(n-i)=n\sum_(i=0)^(n-1)2^i-\sum_(i=0)^(n-1)i2^i`

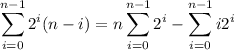
One of these series is geometric and has a well-known closed form:

`\displaystyle\sum_(i=0)^(n-1)2^i=2^n-1`

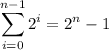
The other (see note below) is a bit less obvious, but can be derived:

`\displaystyle\sum_(i=0)^(n-1)i2^i=2^n(n-2)+2`

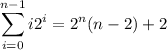
so we have

`a_n=2^n+n(2^n-1)-(2^n(n-2)+2)`

`\implies\boxed{a_n=2^(n+1)+2^n-(n+2)}`

# # #

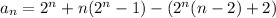
A brief note on how to compute the sum,

`\displaystyle\sum_(i=0)^(n-1)i2^i=2^n(n-2)+2`

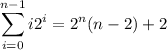
The first term of the sum is 0:

`\displaystyle\sum_(i=0)^(n-1)i2^i=\sum_(i=1)^(n-1)i2^i`

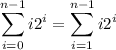
Add and substract 1 to the first factor in the summand and expand the sum into two sums:

`\displaystyle\sum_(i=1)^(n-1)i2^i=\sum_(i=1)^(n-1)(i-1+1)2^i=\sum_(i=1)^(n-1)(i-1)2^i+\sum_(i=1)^(n-1)2^i`

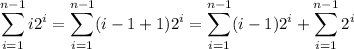
The latter sum we're familiar with. For the other sum, we can shift the index to make it start at
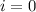`i=0`, and again the first term in the sum would be 0:

`\displaystyle\sum_(i=1)^(n-1)(i-1)2^i=\sum_(i=0)^(n-2)i2^(i+1)=\sum_(i=1)^(n-2)i2^(i+1)`

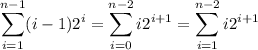
So we have

`\displaystyle\sum_(i=0)^(n-1)i2^i=\sum_(i=1)^(n-2)i2^(i+1)+\sum_(i=1)^(n-2)2^i`

Continuing in this way, we would end up getting

`\displaystyle\sum_(i=0)^(n-1)i2^i=\sum_(i=1)^(n-1)2^i+\sum_(i=2)^(n-1)2^i+\sum_(i=3)^(n-1)2^i+\cdots+\sum_(i=n-2)^(n-1)2^i+\sum_(i=n-1)^(n-1)2^i`

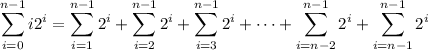
or as a double sum,

`\displaystyle\sum_(i=0)^(n-1)i2^i=\sum_(k=1)^(n-1)\sum_(i=k)^(n-1)2^i`

which is easy to reduce:

`\displaystyle\sum_(i=k)^(n-1)2^i=2^n-2^k`

`\displaystyle\sum_(k=1)^(n-1)(2^n-2^k)=2^n(n-1)-(2^n-2)=2^n(n-2)+2`