1 Answer

Eric Walker · Answer 1 · 2020-04-10T01:26:27+0000

Answer:

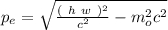
$p_e = \sqrt{ \frac{(\ h \ w \ )^2}{{c^2}} - m_o^2c^2}$

Step-by-step explanation:

If the photons got frequency w, the energy of each photon must be

$E \ = \ h \ w$ ,

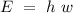so the total energy of the system must be

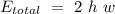$E_(total) \ = \ 2 \ h \ w$ .

The momentum for each photon will be:

$p \ = \ (h \ w)/(c)$ .

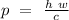But, as they are colliding head on, the total momentum of the system must be zero.

Now, for the particles, the energy must be

$E \ = \ √(p^2c^2 + m_o^2c^4)$ .

Momentum conservation implies that the total momentum must be zero, so:

$| \ \bar{p}_(electron) \ | = | \ \bar{p}_(positron) \ |$ ,

so the squares of the momentum will be the same.

Now, this implies that the energies for the electron and the positron must be the same, so we can write:

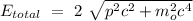$E_(total) \ = \ 2 \ √(p^2c^2 + m_o^2c^4)$ .

Taking conservation of energy in consideration:

$E_(total) \ = \ 2 \ √(p^2c^2 + m_o^2c^4) = \ 2 \ h \ w$ .

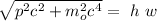$√(p^2c^2 + m_o^2c^4) = \ h \ w$ .

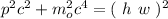$p^2c^2 + m_o^2c^4 = (\ h \ w \ )^2$ .

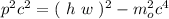$p^2c^2 = (\ h \ w \ )^2 - m_o^2c^4$ .

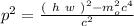$p^2 = ((\ h \ w \ )^2 - m_o^2c^4)/(c^2)$ .

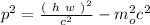$p^2 = \frac{(\ h \ w \ )^2}{{c^2}} - m_o^2c^2$ .

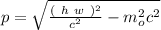$p = \sqrt{ \frac{(\ h \ w \ )^2}{{c^2}} - m_o^2c^2}$ .

And this its the electron's momentum

Please log in or register to add a comment.