Answer:
The 12.1g mass moves at a speed of 10.81 cm/s after the crash and the 12.1g mass moves at a speed of 20.61 cm/s after the crash.
Both masses move to the right because the sign was positive.
Step-by-step explanation:
To solve this problem we apply the theory of shocks:
In an elastic shock the kinetic energy and the amount of linear movement or momentum are conserved.
Because the shock is elastic, the coefficient of elastic restitution (e) is equal to 1.
Principle of conservation of the momentum:
m1vi1+m2vi2=m1vf1+m2vf2 Equation 1
Formula to calculate the coefficient of elastic restitution (e):
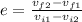Equation 2
m1=12.1 g ,
Vi1= 21cm/s : Initial velocity of the m1
m2=13.1 g
Vi2=11.cm/s: Initial velocity of the m1
v1f: Final velocity of the m1
vf2: Final velocity of the m2
The initial velocities of both masses are to the right then the sign is positive.
We assume that both masses move to the right after the crash, so the sign is positive for the final speeds of both masses.
We replace this information in equation (1) :
12.1 * 21 + 13.1 * 11.2 = 12.1 * vf1 + 13.1 * vf2
254.1 + 146.72 = 12.1 * vf1 + 13.1 * vf2
400.82 = 12.1 * vf1 + 13.1 * vf2 Equation (3)
Because the shock is elastic, the coefficient of elastic restitution (e) is equal to 1,then , we replace this information in equation (2)
9.8 = vf2 - vf1 Equation (4)
Vf2 = vf1 + 9.8 Equation (5)
We replace the equation 5 in the equation (3)
400.82 = 12.1vf1 + 13.1( vf1 + 9.8 ) Equation (3)
400.82 = 12.1vf1 + 13.1vf1 + 13.1 * 9.8
400.82 = 25.2vf1 + 128.38
400.82 - 128.38 = 25.2vf1
272.44 = 25.2vf1
vf1 = (272.44) / (25.2)
vf1 = 10.81 cm/s
We replace vf1 = 10.81 cm/s in the equation (5):
Vf2 = 10,81 + 9.8
Vf2 = 10,81 + 9.8
Vf2 = 20.61cm/s
Answer: The 12.1g mass moves at a speed of 10.81 cm / s after the crash and the 12.1g mass moves at a speed of 20.61 cm/s after the crash.
Both masses move to the right because the sign was positive.