Question

Why is the following situation impossible? A skater glides along a circular path. She defines a certain point on the circle as her origin. Later on, she passes through a point at which the distance she has traveled along the path from the origin is smaller than the magnitude of her displacement vector from the origin.

Answer 1

A skater glides along a circular path. She defines a certain point on the circle as her origin. Later on, she passes through a point at which the distance she has traveled along the path from the origin is smaller than the magnitude of her displacement vector from the origin.

So here in circular motion of the skater we can see that the total path length of the skater is along the arc of the circle while we can say that displacement is defined as the shortest distance between initial and final position of the object.

So it is not possible in any circle that arc-length is less than the chord joining the two points on the circle

As we know that arc length is given as

`L = R\theta`

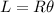
length of chord is given as

`L_c = 2Rsin((\theta)/(2))`

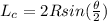
so here

`L > L_c`

`R\theta > 2R sin((\theta)/(2))`

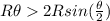
so we have

`(\theta)/(2) > sin((\theta)/(2))`