Question

Clarence wants to estimate the percentage of students who live more than three miles from the school. He wants to create a 98% confidence interval which has an error bound of at most 4%. How many students should be polled to create the confidence interval?

Answer 1

Clarence should poll 847 to create the confidence interval.

Explanation:

We have the following information:

1-α = 0.98

e = 0.04

p = unknown

The value of the sample (n) can be calculated using the following formula:

`n=(z^(2)*p*(1-p) )/(e^(2) )`

First step: obtain the value of p

Since we're not given a value of p, we'll have to use the value that maximizes the sample. The value that maximizes the sample is always p = 0.5.

Second step: obtain the value of z

Since the confidence interval is going to be of 98%, you’ll have 1% of the distribution in each tail. Therefore the z values we’re looking for are the cumulative values of the z distribution up to 1% or up to 99%. Either value will work, but you’ll just need to use one of them.

Looking up on any z-table, the value of a 99% area in a z distribution is of z = 2.327.

Third step: replace in the formula

`n=(z^(2)*p*(1-p) )/(e^(2) ) = (2.327^(2)*0.5*(1-0.5) )/(0.04^(2))=846.08`

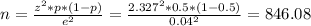
Since we're looking for the number of people that should be polled, we cannot have decimals in the answer. Therefore we round up to 847 students.