Question

An investment of $2,836.05 earns interest at 6.9% per annum compounded monthly for 4 years. At that time the interest rate is changed to 1.7% compounded annually. How much will the accumulated value be three years after the change?

Select one: a. $4,012.89 b. $3,928.25 c. $3,988.47 d. $4,004.88

Answer 1

b. $3,928.25

Step by step explanation:

We use the compound interest formula:

`A=P\left(1+(r)/(n)\right)^(nt)`

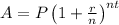
For the first four years:

A is the value of the account after 4 years, so the unknown

P is the investment of $2,836.05

r is the annual rate of 6.9% in decimal form, thus 0.069 (that is 6.9/100)

n is the number of times the interest is compounded per year, thus 12 (since it is compounded monthly)

t is the number of years thus 4

The formula becomes:

`A=2836.05\left(1+(0.069)/(12)\right)^(12(4))`

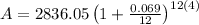
Once we enter that into the calculator, we get:

`A = 3734.53`

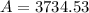
Then that money is invested again for three years further, so we use the very same formula but this time:

A is the value of the account after 3 years, so the unknown

P is the new investment of $3,734.53 that we just got

r is the annual rate which is now 1.7% in decimal form, thus 0.017 (since 1.7/100 is 0.017)

n is the number of times the interest is compounded per year, this time 1 (since it is compounded annually)

t is the number of years thus 3

The formula becomes:

`A=3734.53\left(1+(0.017)/(1)\right)^(1(3))`

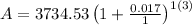
Once we enter that into the calculator, we get:

`A = 3928.25`

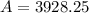
Therefore, the accumulated value by three years after the change will be $3,928.25, thus option b.