Answer:
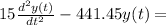 ±
±

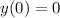 ,
,
Explanation:
See the attached image
This problem involves Newton's 2nd Law which is: ∑F = ma, we have that the acting forces on the mass-spring system are:
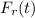 that correspond to the force of resistance on the mass by the action of the spring and
that correspond to the force of resistance on the mass by the action of the spring and
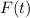 that is an external force with unknown direction (that does not specify in the enounce).
that is an external force with unknown direction (that does not specify in the enounce).
For determinate
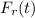 we can use Hooke's Law given by the formula
we can use Hooke's Law given by the formula
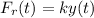 where
where
 correspond to the elastic constant of the spring and
correspond to the elastic constant of the spring and
 correspond to the relative displacement of the mass-spring system with respect of his rest state.
correspond to the relative displacement of the mass-spring system with respect of his rest state.
We know from the problem that an 15 Kg mass stretches the spring 1/3 m so we apply Hooke's law and obtain that...
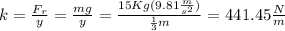
Now we apply Newton's 2nd Law and obtaint that...
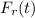 ±
±
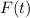 =
=

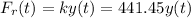
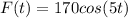
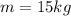

Finally...
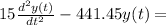 ±
±

We know from the problem that there's not initial displacement and initial velocity, so...
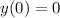 and
and
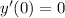
Finally the Initial Value Problem that models the situation describe by the problem is
