Answer:
The concept which best describes the change of the population is the derivative of
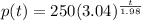 .
.
Explanation:
Observe that the function
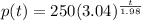 describes the amount of rabbits at the time t (in years) but no the rate of change of the population at a given instant. So you have to use the derivative of
describes the amount of rabbits at the time t (in years) but no the rate of change of the population at a given instant. So you have to use the derivative of
 to obtain that rate of change at any instant. For example, if we derivate the function
to obtain that rate of change at any instant. For example, if we derivate the function
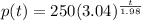 we obtain:
we obtain:
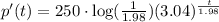
And if we want to find the rate of change at
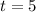 years we evaluate
years we evaluate
 rabbits/year
rabbits/year