Question

The volume of water held by the 2 main ice caps (Antarctica and Greenland) is about 1.6 % the volume of the ocean. What is 1.6 % of the cuboid’s volume (problem 3) in cubic meters? (Use scientific notation and keep 3 significant figures, eg. 1.00E10)

Answer 1

Answer:
`2.14(10)^(16) m^(3)`

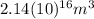
Step-by-step explanation:

Assuming the cuboid has the following dimensions:

Width (W):
`1.9(10)^(7) m`

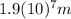
Length (L):
`1.9(10)^(7) m`

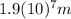
Height (H):
`3700 m`

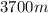
Its volume is:
`V=(W)(L)(H)`

`V=(1.9(10)^(7) m)(1.9(10)^(7) m)(3700m)`

`V=1.34(10)^(18)m^(3)`

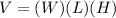
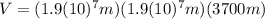
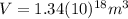
Now, if we want to know what is the
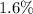`1.6 \%` of this volume, we have to do the following:

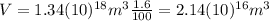`V=1.34(10)^(18)m^(3) (1.6)/(100)=2.14(10)^(16) m^(3)` This is the 1.6 % of the volume of the cuboid