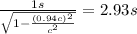Question

Spaceship A is 10 meters long and approaching you from the south at a speed of.7c while spaceship B, which is also 10 meters long, is approaching you from the north at a speed of.7c. a. What is the relative speed of A as measured by B? b. What is the length of A as measured by you? c. What is the length of A as measured by B? d. An event on A lasts 1 second as measured by A. How long does the event last as measured by you? e. An event on A lasts 1 second as measured by A. How long does the event last as measured by B?

Answer 1

a) 0.94 C

b) 7.14 m

c) 3.11 m

d) 1.40 s

e) 2.93 s

Step-by-step explanation:

First we need to set up a coordinate system. This will have the positive X axis pointing north. So spaceship A has positive speed, and spaceship B has negative speed.

The Lorentz transformation for speed is:

`u' = (u - v)/(1 - (u*v)/(c^2))`

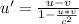
u: speed of spaceship A as observed by you

v: speed of spaceship B as observed by you

In the case of the speed of spaceship A as observed by spaceship B:

`u' = (0.7c - (-0.7c))/(1 - (0.7c*(-0.7c))/(c^2)) = 0.94c`

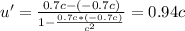
The transform for lengths is:

`L = L0 * \sqrt{1 - (v^2)/(c^2)}`

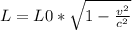
For the case of spaceship A as observed by you:

`L = 10 m * \sqrt{1 - ((0.7c)^2)/(c^2)} = 7.14 m`

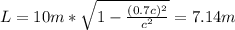
For the case of spaceship A as observed by spaceship B:

`L = 10 m * \sqrt{1 - ((0.94c)^2)/(c^2)} = 3.12 m`

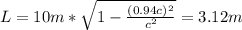
The time dilation equation is:

`T = \frac{T0}{\sqrt{1-(v^2)/(c^2)}}`

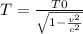
For the case of the event as observed by you:

`\frac{1 s}{\sqrt{1-((0.7c)^2)/(c^2)}} = 1.40 s`

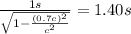
For the case of the event as observed by spaceship B:

`\frac{1 s}{\sqrt{1-((0.94c)^2)/(c^2)}} = 2.93 s`